SVD

✱ Wikipedia: Singular value decomposition

✱ Wikipedia: Décomposition en valeurs singulières

✱ Wikipedia: Lanczos algorithm

✱ Zhaojun Bai, James Demmel, Jack Dongarra, Axel Ruhe, and Henk van der Vorst: Templates for the Solution of Algebraic Eigenvalue Problems: a Practical Guide (SIAM, Philadelphia, 2000)

✱ G. W. Stewart: On the early history of the singular value decomposition (1992)

✱ G. W. Stewart: On the early history of the singular value decomposition (1992) (PDF file)

✱ W. H. Press, B. P. Flannery, S. A. Teukolsky, and W. T. Vetterling
Singular value decomposition
in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge University Press, Cambridge, pp. 51-63, 1992

✱ American Mathematical Society: We recommend a Singular Value Decomposition

✱ Michael E. Wall, Andreas Rechtsteiner, Luis M. Rocha: Singular value decomposition and principal component analysis

✱ SVD tutorial

✱ MIT: Singular value decomposition (SVD) tutorial

✱ Sergey Bochkanov: Singular value decomposition

✱ Professor Strang's linear algebra class lecture videos

✱ Michael W. Berry, Dani Mezher, Bernard Philippe, and Ahmed Sameh: Parallel computation of the singular value decomposition (INRIA, 2003) (PDF file)

✱ Amy N. Langville: An Introduction to Singular Value Decomposition, What does this have to do with search engines?

✱ NAG LAPACK example GitHub Repository: ZGESVD example

✱ NAG: Complex SVD (PDF file)

✱ groups.google: How to do svd for a complex matrix using ublas and lapack bindings?

✱ forum.kde: SVD of a complex matrix

✱ forums.developer.nvidia: Cusolver SVD for general complex matrix

✱ LAPACK: Linear Algebra PACKage (FORTRAN90)

✱ PROPACK: Singular value decomposition of large and sparse or structured matrices

✱ Sabine Van Huffel, C. Decanniere, H. Chen, and P. Van Hecke: Resolution improvement by minimum variance signal enhancement (PDF file)

✱ Y. Coenradie, R. de Beer, D. van Ormondt, H. Ratiney, S. Cavassila, and D. Graveron-Demilly: Background-signal parameterization in in vivo MR spectroscopy (PDF file)

✱ Wing Yiu CHOY, Bryan C. Sanctuary (advisor): Using numerical methods and artificial intelligence in NMR data processing and analysis (PDF file)

✱ Ondřej Nikel, Danielle Laurencin, Christian Bonhomme, Grażyna E. Sroga, Silke Besdo, Anna Lorenz, and Deepak Vashishth
Solid state NMR investigation of intact human bone quality: Balancing issues and insight into the structure at the organic−mineral interface,
J. Phys. Chem. C 116, 6320-6331 (2012).
Abstract

✱ Babak Alipanahi, Xin Gao, Emre Karakoc, Logan Donaldson and Ming Li
PICKY: a novel SVD-based NMR spectra peak picking method,
Bioinformatics 25, i268-i275 (2009).
Abstract (PDF)

✱ Xin Wang and Jing-Huei Lee
IRIS-HSVD algorithm for automatic quantitation of in vivo ³¹P MRS,
J. Magn. Reson. 196, 23-32 (2009).
Abstract

✱ Nikola Trbovic, Serge Smirnov, Fengli Zhang and Rafael Brüschweiler
Covariance NMR spectroscopy by singular value decomposition,
J. Magn. Reson. 171, 277-283 (2004).
Abstract

✱ Osama A. Ahmed and Moustafa M. Fahmy
NMR signal enhancement via a new time-frequency transform,
IEEE Trans. Med. Imaging 20, 1018-1025 (2001).
Abstract

✱ Osama A. Ahmed
Fast computation of discrete SLTF transform,
in Proceedings of the 11th IEEE Workshop on Statistical Signal Processing
Orchid Country Club, Singapore, 20, 317-320 (2001).

✱ Guang Zhu, Wing Y. Choy, Guoqiang Song, and B. C. Sanctuary
Suppression of diagonal peaks with singular value decomposition,
J. Magn. Reson. 132, 176-178 (1998).
Abstract

✱ Douglas E. Brown and Thomas W. Campbell
Enhancement of 2D NMR spectra using singular value decomposition,
J. Magn. Reson. 89, 255-264 (1990).
Abstract

✱ H. Barkhuijsen, R. de Beer, and D. van Ormondt
Improved algorithm for noniterative time-domain model fitting to exponentially damped magnetic resonance signals,
J. Magn. Reson. 73, 553-557 (1987).
Abstract

SVD with cuSolver

✱ OrangeOwlSolutions, Linear-Algebra

✱ ernestyalumni, CompPhys

SVD with Java

✱ Eff + Java = ?

✱ JAMA: A Java matrix package

✱ G. W. (Pete) Stewart: JAMPACK (A Java package for matrix computations)

✱ Princeton: SVD.java

✱ Drexel: The dragon toolkit

Online tool

✱ Online Singular value decomposition

✱ Online Matrix calculator

Java library

✱ Michael Thomas Flanagan's Java scientific library: Fourier Transforms

✱ Richard G. Baldwin: 2D Fourier transforms using Java

✱ Steven W. Smith: The scientist and engineer's guide to digital signal processing

✱ Forest Products Laboratory: Linear algebra for statistics Java package

✱ JavaNumerics: A focal point for information on numerical computing in Java

Toeplitz matrix

✱ Wikipedia: Toeplitz matrix is a matrix in which each descending diagonal from left to right is constant:

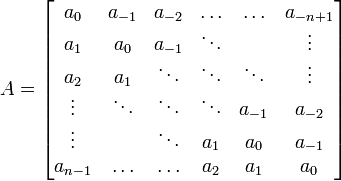
✱ Andrew E. Yagle
A new algorithm for the nearest singular Toeplitz matrix to a given Toeplitz matrix, (PDF)

Hankel matrix

✱ Wikipedia: Hankel matrix

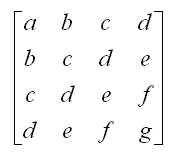
A matrix in which each descending diagonal from right to left is constant

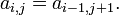
✱ Fast general Hankel/Toeplitz SVD package (MatLab)

✱ Xuezhi Zhao and Bangyan Ye
Similarity of signal processing effect between Hankel matrix-based SVD and wavelet transform and its mechanism analysis,
Mechanical Systems and Signal Processing 23, 1062-1075 (2009).
Abstract

✱ Kevin Browne, Sanzheng Qiao, and Yimin Wei
A Lanczos bidiagonalization algorithm for Hankel matrices,
Linear Algebra Appl. 430, 1531-1543 (2009).
Abstract

For any square complex Hankel matrix A of order n, there exist a unitary Q and an order n nonnegative diagonal Σ such that A = QΣQ^T.

✱ Wei Xua and Sanzheng Qiao
A fast symmetric SVD algorithm for square Hankel matrices ,
Linear Algebra Appl. 428, 550-563 (2008).
Abstract

✱ Vadim Olshevsky and Michael Stewart
Stable factorization for Hankel and Hankel-like matrices,
Numer. Linear Algebra Appl. 189, 401-434 (2001).
Abstract

✱ Ye Li, K. J. Ray Liu, and J. Razavilar
A parameter estimation scheme for damped sinusoidal signals based on low-rank Hankel approximation,
IEEE Trans. Signal Processing 45, 481-486 (1997).
Abstract

✱ Peter Strobach
Square Hankel SVD subspace tracking algorithms,
Signal Process. 57, 1-18 (1997).

For a real square N x N Hankel data matrix, left and right orthonormal matrices are identical.

✱ Rémy Boyer and Roland Badeau
Adaptive multilinear SVD for structured tensors, (PDF)

✱ Timothy M. Toolan and Donald W. Tufts
Detection and estimation in non-stationary environments, (PDF)

✱ D. L. Boley, F. T. Luk, and D. Vandevoorde
Vandermonde factorization of a Hankel matrix, (PDF)

Cadzow procedure

✱ Simon Poulding, Adrian J. Charlton, James Donarski, and Julie C. Wilson
Removal of t1 noise from metabolomic 2D 1H-13C HSQC NMR spectra by correlated trace denoising,
J. Magn. Reson. 189, 190-199 (2007).
Abstract

✱ Sharif D. Kunikeev, Howard S. Taylor, Thorsten Schroer, Ralf Haiges, C. J. Bigler Jones, and Karl O. Christe
New signal processing method for the faster observation of natural-abundance ¹⁵N NMR spectra and its application to N₅⁺,
Inorg. Chem. 45, 437-442 (2006).
Abstract

✱ Sharif D. Kunikeev, Howard S. Taylor, Jian-Jung Pan, Allan Kershaw, and Charles E. McKenna
A new signal processing method to observe weak ³¹P and ¹⁷O NMR peaks,
J. Organomet. Chem. 690, 2644-2650 (2005).
Abstract

✱ Alexey L. Kaledin, Sharif D. Kunikeev, and Howard S. Taylor
An accurate theoretical prediction of the zero point vibrational energy of CH₅⁺,
J. Phys. Chem. A 108, 4995-4997 (2004).
Abstract

✱ Sharif D. Kunikeev and Howard S. Taylor
Saving measurement time in 13C NMR spectroscopy,
J. Phys. Chem. A 108, 743-753 (2004).
Abstract

✱ Sharif D. Kunikeev, Erdinç Atilgan, Howard S. Taylor, Alexey L. Kaledin, and Jörg Main
An application of error reduction and harmonic inversion schemes to the semiclassical calculation of molecular vibrational energy levels,
J. Chem. Phys. 120, 6478-6486 (2004).
Abstract

✱ Stewart Trickett
F-x eigen noise suppression,
CSEG Geophysics 2002 PDF file

✱ Caroline Brissac, Thérèse E. Malliavin, and Marc A. Delsuc
Use of the Cadzow procedure in 2D NMR for the reduction of t1 noise,
J. Biomol. NMR 6, 361-365 (1995).
Abstract

✱ A. Diop, Y. Zaim-Wadghiri, A. Briguet, and D. Graveron-Demilly
Improvements of quantitation by using the Cadzow enhancement procedure prior to any linear-prediction methods,
J. Magn. Reson. B 105, 17-24 (1994).
Abstract

✱ Y. Y. Lin and L. P. Hwang
NMR signal enhancement based on matrix property mappings,
J. Magn. Reson. A 103, 109-114 (1993).
Abstract

✱ A. Diop, A. Briguet, and D. Graveron-Demilly
Automatic in vivo nmr data processing based on an enhancement procedure and linear prediction method,
Magn. Reson. Med. 27, 318-328 (1992).
Abstract

✱ J. A. Cadzow
Signal enhancement–A composite property mapping algorithm,
IEEE Trans. Acoustics, Speech, and Signal Processing 36, 49-62 (1988).
Abstract

✱ J. A. Cadzow
Spectral estimation: An overdetermined rational model equation approach,
Proceedings IEEE 70, 907-939 (1982).
Abstract

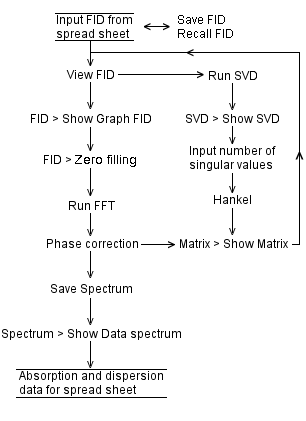
Java applet performing SVD of a complex Hankel matrix: Denoising an FID

The size (600 complex numbers) of an FID (free-induction decay) signal is limited by the web browser. With a 3-GHz processor, the singular value decomposition of the associated complex Hankel matrix takes about 40 seconds.

It is simpler to input the real and imaginary values of the FID into two columns of a spreadsheet program such as MS EXCEL, then copy and paste each data column into the Java applet.

The fast Fourier transform of an FID requires a power of two for the number of complex numbers in an FID, therefore zero-filling the FID before FFT.

Java does not allow us to paste external data into an applet. We provide the corresponding fidsvd applet for local use, outside a web browser: download. The change of color of View FID button from red to green after clicking Run SVD button means the number of iterations for singular value decomposition has reached its maximum. As a result, close then restart the applet. Provide a shorter FID. Here is an MS Excel spread sheet containing simulated FIDs. The SVD of 1000 complex numbers takes about 180 seconds.

Spectrum from denoised 29-Si MAS FID by SVD

Comparison of spectra obtained from FID traited by line broadening with that obtained from the same FID denoised by SVD:

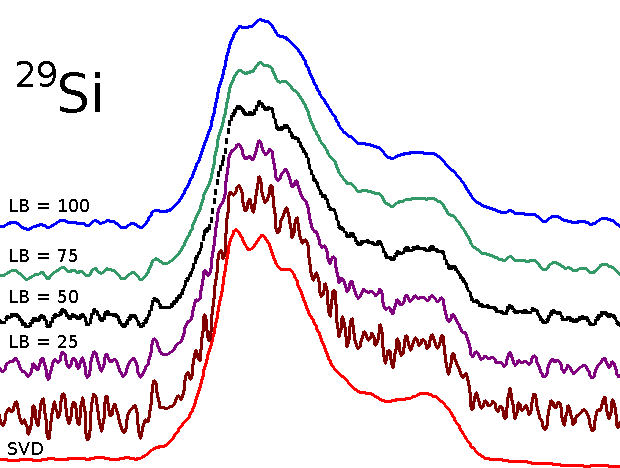
Spectrum obtained from denoised FID by SVD presents better resolution.

Signal and noise

✱ Lionel Chiron, Maria A. van Agthoven, Bruno Kieffer, Christian Rolando, and Marc-André Delsuc
Efficient denoising algorithms for large experimental datasets and their applications in Fourier transform ion cyclotron resonance mass spectrometry,
Proc. Natl. Acad. Sci. USA 111, 1385-1390 (2014).
Abstract

✱ Stevens Institute for Innovation, University of Southern California, 2009
“Denoising 1D solution NMR (DSNMR)” fewer transients - more sensitivity magnet resonance analysis by Singular Value Decomposition Harmonic Inversion,
PDF file

✱ François Chapeau-Blondeau and David Rousseau
Raising the noise to improve performance in optimal processing,
J. Stat. Mech: Theory Exp. P01003 (2009).
Abstract

✱ Christoph Kaiser, Jakob J. Lopez, Wolfgang Bermel, and Clemens Glaubitz
Dual transformation of homonuclear solid-state NMR spectra—an option to decrease measuring time,
Biochim. Biophys. Acta, Biomembr. 1768, 3107-3115 (2007).
Abstract

✱ Ulrich L. Günther
Advanced NMR Processing,
EuroLabCourse "Advanced Computing in NMR Spectroscopy", Florence, Sept. 2001
Presentation PDF file, Lecture notes PDF file

✱ Ulrich L. Günther, Christian Ludwig, and H. Rüterjans
NMRLAB—Advanced NMR data processing in Matlab,
J. Magn. Reson. 145, 201-208 (2000).
Abstract

✱ Martin Vetterli: Sparse sampling: Variations on a theme by Shannon