Analytical expression of W(4,0) for static crystal in NMR
The second-order quadrupole interaction is related to W(4,0):
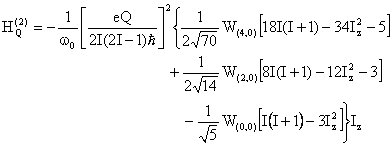
In static NMR experiment, W(4,0) is defined by:
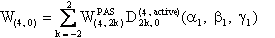
Its analytical expression can be determined as follows:
(1) Select and copy the following green lines; then paste them into a cell of Mathematica, a software for numerical and symbolic calculations.
(2) Press "Ctrl-A" for select all; then
press "Shift-enter" for evaluate cells.
(Or in the menu bar, select Kernel > Evaluation > Evaluate Cells)
Using Mathematica-5 running with a 3-GHz processor, the analytical expression of W(4,0) is obtained in 5 seconds.
(* W4pas is a row-matrix with 5 columns
containing the 5 nonzero eigenvalues of the EFG
expressed as a 4-th rang spherical tensor, in (eq)(eq) unit *)
W4pas = {{eta*eta/4, 3*eta/(2*Sqrt[7]), (9 + eta*eta/2)/Sqrt[70],
3*eta/(2*Sqrt[7]), eta*eta/4}};
(* D4 is a reduced form (5 rows x 1 column) of the 4-th order
Wigner active rotation matrix *)
D4 = {
{Sqrt[35/2]*Sin[beta1]^4*E^(-4*I*alpha1)/8},
{Sqrt[5/2]*(-1 +7*Cos[beta1]^2)*Sin[beta1]^2*E^(-2*I*alpha1)/4},
{(3 - 30*Cos[beta1]^2 + 35*Cos[beta1]^4)/8},
{Sqrt[5/2]*(-1 +7*Cos[beta1]^2)*Sin[beta1]^2*E^(2*I*alpha1)/4},
{Sqrt[35/2]*Sin[beta1]^4*E^(4*I*alpha1)/8}
};
(* W40static is an expression *)
W40static = FullSimplify[W4pas.ComplexExpand[D4]];
(* suppression of the double curve brackets {{}} of W40static *)
Print[W40static[[1, 1]]];
Remove[W4pas, eta, D4, alpha1, beta1, W40static];
