EFG tensor for rotating crystal

For rotating crystal, two axis-systems are involved. One orientates the static magnetic field B₀ in the rotor-axis system (轉子坐標系, x_VAS, y_VAS, z_VAS). The second orientates the rotor in the principal-axis system (主軸坐標系) of the EFG tensor (X_PAS, Y_PAS, Z_PAS).

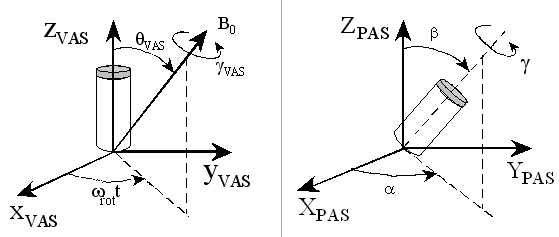
In fact, NMR rotor performs positive or right-hand rotation around its z_VAS axis. Since the rotor spinning rate ω_rot is a positive number by definition, a minus sign must appear with the first Euler angle, that is, -ω_rot*t in the above figure. [see O. N. Antzutkin; Sideband manipulation in magic-angle-spinning nuclear magnetic resonance, Prog. Nucl. Magn. Reson. Spectrosc. 35, 203-266 (1999)]

As a result, analytical expressions containing the rotor spinning rate (in quadrupole interaction web pages of this site) must change its sign.

(A) Variable-Angle-Spinning experiment 變角旋轉

(1) V_(2,0) tensor component

The component V_(2,0) in the observation frame is related to the eigen values of V by the following two relations:

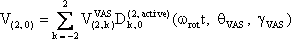
and

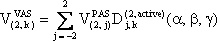
We provide a Mathematica notebook that calculates the component V_(2,0) of the second-rank spherical tensor V, whose final expression is:

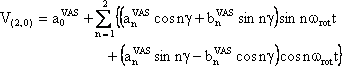
with

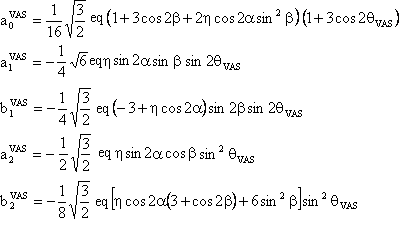
(2) W_(2,0) tensor component

The component W_(2,0) in the observation frame is related to the eigen values of W by the following two relations:

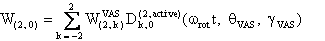
and

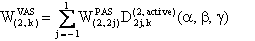
We also provide a Mathematica notebook that calculates the component W_(2,0) of the fourth-rank spherical tensor W, whose final expression is:

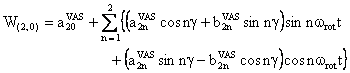
with

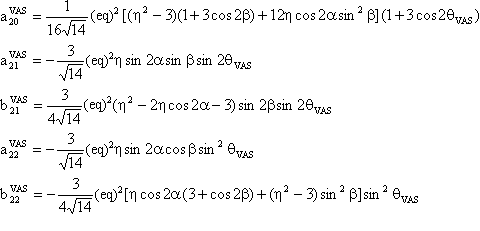
(3) W_(4,0) tensor component

The component W_(4,0) in the observation frame is related to the eigen values of W by the following two relations:

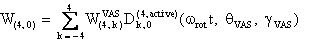
and

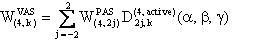
We also provide a Mathematica notebook that calculates the component W_(4,0) of the fourth-rank spherical tensor W, whose final expression is:

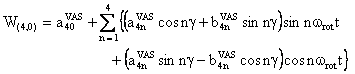
with

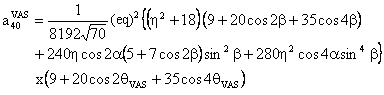
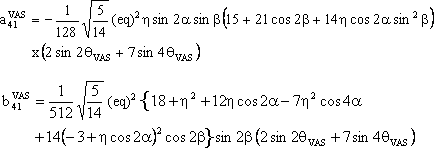
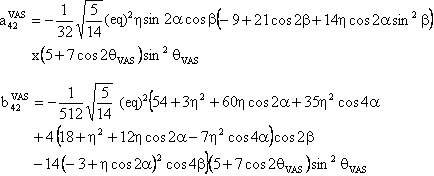
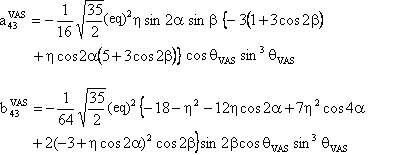
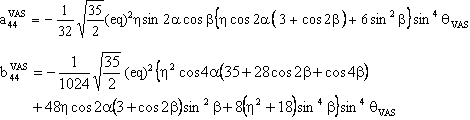
(B) Magic-Angle-Spinning experiment 魔角旋轉

In practice, the angle θ_VAS of the rotor is the magic-angle with:
θ_VAS = θ_MAS = arccos{sqrt(1/3)}.

(1) V_(2,0) tensor component

The component V_(2,0) has the following form:

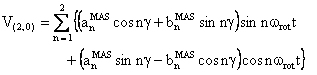
with

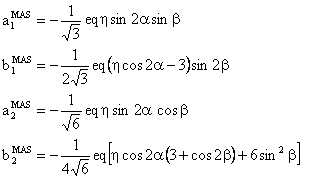
(2) W_(2,0) tensor component

The component W_(2,0) has the following form:

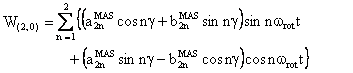
with

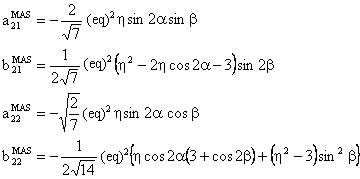
(3) W_(4,0) tensor component

The component W_(4,0) has the following form:

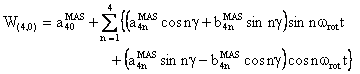
with

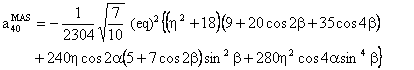
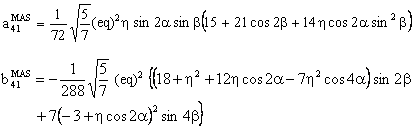
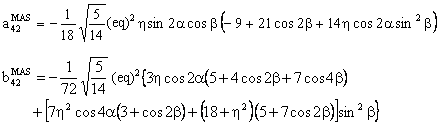
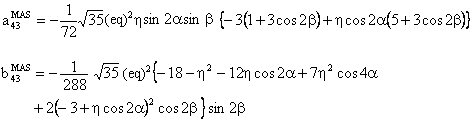
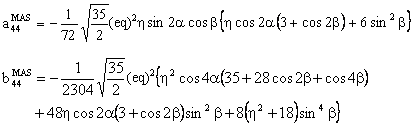
(C) Conclusion

In the above expressions, the asymmetry parameter η is associated with cos2α or with sin2α. As a result, if we add π/2 to α, η will change to -η . In other words, the passage from our convention for η to that used in the simulation program SIMPSON and vice-versa is the addition of π/2 to the Euler angle α. [see J. M. Koons, E. Hughes, H. M. Cho, and P. D. Ellis; Extracting multitensor solid-state NMR parameters from lineshapes, J. Magn. Reson. A 114, 12-23 (1995)]

However, if a software allows us to change the sign of η, we should use this possibility instead of adding π/2 to the Euler angle α.