Analytical expression of W(2,0) for rotating crystal in VAS and MAS NMR
The second-order quadrupole interaction is related to W(2,0):
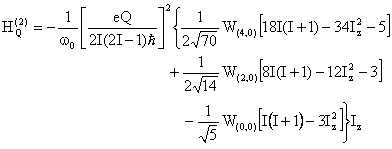
In VAS (MAS) NMR experiments, W(2,0) is defined by:
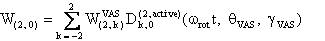
with
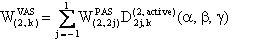
The final expression of W(2,0) in VAS (MAS) NMR is:
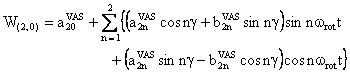
The analytical expressions of a20, a2n, and b2n coefficients can be determined as follows:
(1) Select and copy the following green lines; then paste them into a cell of Mathematica, a software for numerical and symbolic calculations.
(2) Press "Ctrl-A" for select all; then
press "Shift-enter" for evaluate cells.
(Or in the menu bar, select Kernel > Evaluation > Evaluate Cells)
Using Mathematica-5 running with a 3-GHz processor, some spelling error messages followed by the analytical expression of coefficients involved in W(2,0) for VAS and MAS NMR are obtained in 15 seconds.
(* D2 is a reduced form (5 rows x 3 columns) of the 2-nd order
Wigner active rotation matrix *)
D2 = {
{ (1 + Cos[beta])^2*E^(-I*(2*alpha + 2*gamma))/4,
-(1 + Cos[beta])*Sin[beta]*E^(-I*(2*alpha + gamma))/2,
Sqrt[3/8]*Sin[beta]^2*E^(-2*I*alpha),
-(1 - Cos[beta])*Sin[beta]*E^(-I*(2*alpha - gamma))/2,
(1 - Cos[beta])^2*E^(-I*(2*alpha - 2*gamma))/4},
{ Sqrt[3/8]*Sin[beta]^2*E^(-2*I*gamma),
Sqrt[3/8]*Sin[2*beta]*E^(-I*gamma),
(-1 + 3*Cos[beta]^2)/2,
-Sqrt[3/8]*Sin[2*beta]*E^(I*gamma),
Sqrt[3/8]*Sin[beta]^2*E^(2*I*gamma)},
{ (1 - Cos[beta])^2*E^(I*(2*alpha - 2*gamma))/4,
(1 - Cos[beta])*Sin[beta]*E^(I*(2*alpha - gamma))/2,
Sqrt[3/8]*Sin[beta]^2*E^(2*I*alpha),
(1 + Cos[beta])*Sin[beta]*E^(I*(2*alpha + gamma))/2,
(1 + Cos[beta])^2*E^(I*(2*alpha + 2*gamma))/4}
};
MatrixForm[D2];
(* W2pas is a row-matrix with 3 columns
containing the 3 nonzero eigenvalues of the EFG
expressed as a 2-nd rang spherical tensor, in (eq)(eq) unit *)
W2pas = {{Sqrt[3/7]*eta, (eta*eta - 3)/Sqrt[14], Sqrt[3/7]*eta}};
MatrixForm[W2pas];
(* W2k is a row-matrix with 5 columns *)
W2k = W2pas.ComplexExpand[D2];
(* D2VAS is a reduced form (5 rows x 1 column) of the 2-nd order
Wigner active rotation matrix *)
D2VAS = {
{Sqrt[3/8]*Sin[thetaVAS]^2*E^(-2*I*rot*t)},
{-Sqrt[3/8]*Sin[2*thetaVAS]*E^(-I*rot*t)},
{(-1 + 3*Cos[thetaVAS]^2)/2},
{Sqrt[3/8]*Sin[2*thetaVAS]*E^(I*rot*t)},
{Sqrt[3/8]*Sin[thetaVAS]^2*E^(2*I*rot*t)}
};
MatrixForm[D2VAS];
(* W20vas is an expression *)
W20vas = W2k.ComplexExpand[D2VAS];
m1 = Expand[W20vas] /. {Cos[a_ + b_] -> Cos[a] Cos[b] - Sin[a] Sin[b],
Sin[a_ + b_] -> Cos[b] Sin[a] + Cos[a] Sin[b]};
m2 = Collect[m1, {Cos[x_ *rot*t], Sin[y_ *rot*t],
Cos[rot*t], Sin[rot*t] }];
(* suppression of the double curve brackets {{}} of m2 *)
m22 =m2[[1,1]];
size = Length[m22];
(* a22VAS = amplitude of Cos[2*gamma]*Sin[2*rot*t] *)
a22VAS = FullSimplify[Coefficient[m22[[size - 3, 2]], Cos[2*gamma]]];
a22MAS = FullSimplify[a22VAS /. thetaVAS -> ArcCos[Sqrt[1/3]]];
(* b22VAS = amplitude of Sin[2*gamma]*Sin[2*rot*t] *)
b22VAS = FullSimplify[Coefficient[m22[[size - 3, 2]], Sin[2*gamma]]];
b22MAS = FullSimplify[b22VAS /. thetaVAS -> ArcCos[Sqrt[1/3]]];
(* a21VAS = amplitude of Cos[gamma]*Sin[rot*t] *)
a21VAS = FullSimplify[Coefficient[m22[[size - 1, 2]], Cos[gamma]]];
a21MAS = FullSimplify[a21VAS /. thetaVAS -> ArcCos[Sqrt[1/3]]];
(* b21VAS = amplitude of Sin[gamma]*Sin[rot*t] *)
b21VAS = FullSimplify[Coefficient[m22[[size - 1, 2]], Sin[gamma]]];
b21MAS = FullSimplify[b21VAS /. thetaVAS -> ArcCos[Sqrt[1/3]]];
(* c22VAS = amplitude of Cos[2*gamma]*Cos[2*rot*t]*)
(* c22VAS = -b22VAS *)
c22VAS = FullSimplify[Coefficient[m22[[size - 2, 2]], Cos[2*gamma]]];
(* d22VAS = amplitude of Sin[2*gamma]*Cos[2*rot*t] *)
(* d22VAS = a22VAS *)
d22VAS = FullSimply[Coefficient[m22[[size - 2, 2]], Sin[2*gamma]]];
(* c21VAS = amplitude of Cos[gamma]*Cos[rot*t] *)
(* c21VAS = -b21VAS *)
c21VAS = FullSimplify[Coefficient[m22[[size, 2]], Cos[gamma]]];
(* d21VAS = amplitude of Sin[gamma]*Cos[rot*t] *)
(* d21VAS = a21VAS *)
d21VAS = FullSimplify[Coefficient[m22[[size, 2]], Sin[gamma]]];
(* a20VAS *)
a20VAS = FullSimplify[Sum[m22[[i]], {i, 1, size - 4}]];
a20MAS = FullSimplify[a20VAS /. thetaVAS -> ArcCos[Sqrt[1/3]]];
(*--------------- Table of a2jVAS and b2jVAS for VAS --------------*)
tableW20VAS = List[{"a20VAS", a20VAS},
{"a21VAS", a21VAS}, {"b21VAS", b21VAS},
{"a22VAS", a22VAS}, {"b22VAS", b22VAS}];
Print[TableForm[tableW20VAS,
TableHeadings ->
{None, {"VAS", "expression of a2jVAS and b2jVAS in VAS"}}]];
Print["******************************************"];
(*--------------- Table of a2jMAS and b2jMAS for MAS --------------*)
tableW20MAS = List[{"a20MAS", a20MAS},
{"a21MAS", a21MAS}, {"b21MAS", b21MAS},
{"a22MAS", a22MAS}, {"b22MAS", b22MAS}];
Print[TableForm[tableW20MAS,
TableHeadings ->
{None, {"MAS", "expression of a2jMAS and b2jMAS in MAS"}}]];
Remove[D2, alpha, beta, gamma, W2pas, eta, W2k, D2VAS, thetaVAS,
rot, t, W20vas, m1, m2, m22, size, a22VAS, a21VAS, a20VAS,
b22VAS, b21VAS, c22VAS, c21VAS, d22VAS, d21VAS, a22MAS,
a21MAS, a20MAS, b22MAS, b21MAS, c22MAS, c21MAS, d22MAS,
d21MAS, tableW20VAS, tableW20MAS];
