Amplitude-modulated two-pulse MQMAS
AIM: We provide Mathematica-5 notebooks to optimize the echo and antiecho amplitudes for two-pulse MQMAS NMR experiment applied to half-integer quadrupole spin.
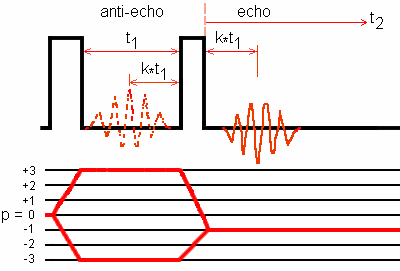
Fig. 1: Amplitude-modulated two-pulse MQMAS sequence and coherence
transfer pathways for 3Q echo and -3Q antiecho of a spin I = 5/2 system.
0Q -> 3Q -> -1Q is the 3Q echo transfer pathway.
0Q -> -3Q -> -1Q is the -3Q antiecho transfer pathway.
The echo amplitude and the antiecho amplitude have opposite signs.
Method: We simulate the echo and the antiecho amplitudes of a spin I = 5/2 versus a pulse duration in a powder rotating at the magic angle, using Mathematica-5 notebooks.
The parameters for these simulations are:
- Nucleus: 27Al
- Spin: 5/2
- 27Al Larmor frequency: 208.61889974 MHz
- Proton Larmor frequency: 800 MHz
- Only 3Q and -3Q coherences belonging to the second diagonal of the density matrix are taken into account for the simulation
- Amplitude of the radio-frequency pulse: 100 kHz
- Pulse duration increment: 0.25 μs
- Number of pulse duration increment: 17
- Rotor spinning speed: 15 kHz
- Quadrupole interaction: first and second orders
- Quadrupole coupling constant: 5 MHz
- Asymmetry parameter: 1
- Crystal file: rep100_simp
- Number of summation steps of the Euler angle γ of the rotor: 10
(A) Mathematica-5 notebook
(1) Preliminary
| Optimization with |
Notebook | SIMPSON 1.1.1 |
|---|---|---|
| p1 for both pathways |
both_P1 (pdf) | both_P1 |
| p2 for both pathways |
both_P2 (pdf) | both_P2 |
| p2 for echo pathway |
echo_P2 (pdf) | echo_P2 |
| p2 for antiecho pathway |
antiecho_P2 (pdf) | antiecho_P2 |
- Download Mathematica-5 notebooks, that for MAS NMR utilities QUADRUPOLE_1_0.nb (the corresponding PDF file), and the crystal file rep100_simp.
- Save these files into the software Mathematica-5 folder. Forbidden the Operating System of your computer to include extra file extension to rep100_simp by providing the file name with double quotes such as "rep100_simp".
- Open QUADRUPOLE_1_0.nb file with Mathematica-5.
- Press "Ctrl-A" to select the notebook, then press "Shift-enter" to start the notebook. (Some warning messages appear but they have no consequences on the results.) A new file called QUADRUPOLE is created in Mathematica-5 folder.
(2) Simulation
- Open a file such as twoPulse_P2.nb file with Mathematica-5.
- Press "Ctrl-A" to select the notebook, then press "Shift-enter" to start simulation. At the end a data file, called twoPulse_P2, is created in Mathematica-5 folder. MS Excel can open this data file for graphic representation.
(B) Result
Figures 2 to 4 represent simulated data.
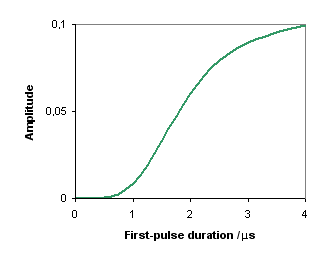
Fig. 2: Sum of 3Q echo and -3Q antiecho amplitudes of 27Al versus the first-pulse duration. The second-pulse duration is 1 μs. Notebook filename: twoPulse_P1.nb.
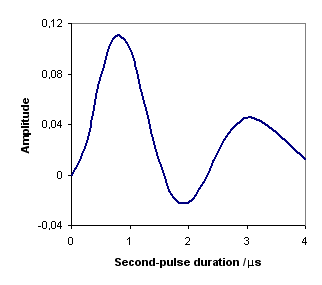
Fig. 3: Sum of 3Q echo and -3Q antiecho amplitudes of 27Al versus the second-pulse duration. The first-pulse duration is 4 μs. Notebook filename: twoPulse_P2.nb.
Figure 2 shows that the amplitude varies monotonously when the first-pulse duration increases. In contrast, Fig. 3 shows that the amplitude changes signs twice for the same range of the second-pulse duration.
From an experimental point of view, these two curves suggest us to
optimize the amplitude in the following way:
(1) by varying the second-pulse duration
and providing a first-pulse duration of a few μs;
(2) by varying the first-pulse duration and fixing the duration of the
second pulse to that obtained in step (1).
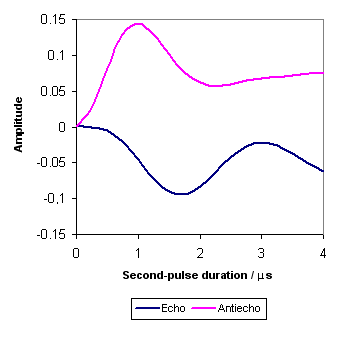
Fig. 4: 27Al 3Q echo amplitude and -3Q antiecho amplitude versus the second-pulse duration. The first-pulse duration is 4 μs. Notebook filenames: twoPulseEcho_P2.nb and twoPulseAntiecho_P2.nb.
The extreme value of -3Q antiecho curve is larger than that of 3Q echo curve.
(C) Conclusion
The different behavior of the 3Q echo and -3Q antiecho amplitudes of a spin I = 5/2 versus the pulse duration (Fig. 4) is due to the fact that the two coherence transfer pathways are not symmetrical. The coherence order change from p = 3 to p = -1 is four for the echo pathway whereas that from p = -3 to p = -1 is two for the antiecho pathway. This leads to 2-dimensional pure absorption lineshape distortions.
