XSLT numerical search of cogwheel phase cycling parameters

In the XML modelling steps, we have generated the mqmas.xml file on WINDOWS desktop. Now we associate an XSLT (eXtensible Stylesheet Language Transformation) file called mqmas.xsl with the mqmas.xml file to search the winding numbers satisfying the condition:

(w_{B} - w_{A}) (p_{AB} - p_{AB}^{0}) + (w_{C} - w_{B}) (p_{BC} - p_{BC}^{0})

= N x integer.

It is equivalent to the condition:

(w_{B} - w_{A}) (p_{AB} - p_{AB}^{0}) + (w_{C} - w_{B}) (p_{BC} - p_{BC}^{0})

mod N = 0, mod being the modulus operator.

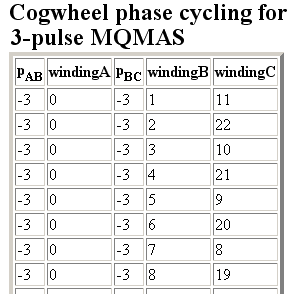
For the antiecho coherence transfer pathway 0Q -> 3Q -> 1Q -> -1Q ( $p_{AB}^{0}$ = 3 and $p_{BC}^{0}$ = 1 for this 3QMAS sequence), Levitt and coworkers found N = 23. It is well known from nested phase cycling procedure that one of the pulse phases can be zero. We choose to set the winding number of the first pulse to zero, $w_{A}$ = 0.

Step 1: Download mqmas.xsl on WINDOWS desktop

By downloading mqmas.xsl, we have two files on WINDOWS desktop.

Step 2: Numerical search

By clicking the mqmas.xml file with the mouse, the default web browser starts. Then it presents a 5-column table. In order to save this table for further analyses, first we select and copy the web page, then paste the data in an MS EXCEL spreadsheet.

Split-t1 MQMAS

Z-filter MQMAS