Quadrupole interaction and electric-field gradient tensor.
四極矩作用力
與 電場梯度張量
Contributor: Y. Millot
[an error occurred while processing this directive]
Quadrupole interaction in a uniform space
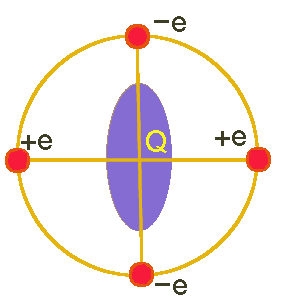
Quadrupole nuclei with a half-integer spin larger than 1/2 possess a quadrupole moment Q, which interacts with the electric-field gradient (EFG) generated by their surroundings.
The coupling of Q (a property of the nucleus) with an EFG (a property of a sample) is called the quadrupole interaction (四極矩作用力).
(A) Quadrupole interaction in Cartesian tensor representation 笛卡爾張量形式
Consider a free nucleus in a uniform space,
that is, the three coordinate axes x, y, and z are equivalent.
The Hamiltonian representing the quadrupole interaction
of this nucleus, independent of the Cartesian coordinate frame,
is defined by:
![]()
where Vjk are the Cartesian components of
V, the EFG at the origin, which is a second-rank
symmetrical tensor. In the principal-axis system of the EFG
(XPAS, YPAS, ZPAS),
V is diagonal:
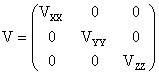
with the convention
![]()
However, another convention is also often used (for example in the
NMR simulation program SIMPSON):
Furthermore, the Laplace equation,
VXX + VYY + VZZ = 0,
holds for V, because the electric field
at the nucleus is produced by charges wholly external to the
nucleus. Thus, only two independent parameters are required:
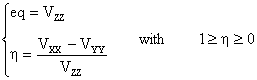
the largest component (最大的梯度) and the asymmetry parameter
(不對稱參數), respectively.
For SIMPSON, these two parameters become:
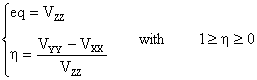
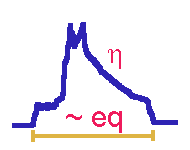
In practice, the asymmetry parameter η defines the powder lineshape and eq is related to the linewidth.
The product of eq with eQ divided by Planck's constant is called the quadrupole coupling constant (Cq) 四極偶合常數.
In the principal-axis system of V,
the quadrupole interaction takes the form:
![]()
In term of the operators (算子)
I+ = IX + iIY
and I- = IX - iIY,
the quadrupole interaction becomes:
(B) Quadrupole interaction in spherical tensor representation 球張量形式
The passage from one coordinate frame to another is more conveniently realized if the quadrupole interaction of a free nucleus is expressed as a product of second-rank irreducible spherical tensors:
In any Cartesian coordinate frame, the spherical tensor and
Cartesian tensor components of V and
T are related by:
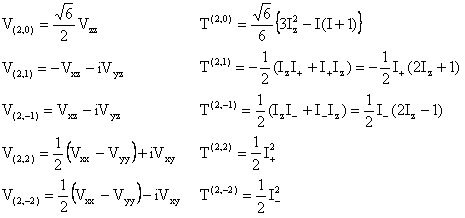
with I+ = Ix + iIy and
I- = Ix - iIy. These two
operators are different from those used previously despite
the same notation. The numerical factors in the components
of V and T depend on the
authors. The spherical tensor representation of the
quadrupole interaction becomes:
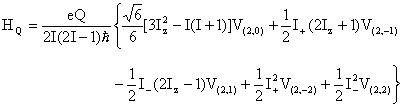
Expressing the latter Hamiltonian in the principal-axis system of the EFG tensor and comparing the result with the last expression of quadrupole interaction in Cartesian tensor section yield the spherical tensor components of V in the principal-axis system:
(C) References
- Wikipedia: Covariance and contravariance of vectors
- Wikipedia: Tensor
- Roy McWeeny: Tensor Techniques in Physics – a concise introduction
- Kees Dullemond and Kasper Peeters: Introduction to tensor calculus
- R. A. Sharipov:
Quick Introduction to Tensor Analysis
Rule 5.3. For any double indexed array with indices on the same level (both upper or both lower) the first index is a row number, while the second index is a column number. If indices are on different levels (one upper and one lower), then the upper index is a row number, while lower one is a column number.
- Michael Fowler, University of Virginia: Tensor operators
- Berkeley: Irreducible tensor operators and the Wigner-Eckart theorem
- Ivan Deutsch, University of New Mexico: Irreducible tensor operators and the Wigner-Eckart theorem
- University of Tennessee, Knoxville: The Wigner-Eckart theorem
(D) Mathematica-5 notebook
- Double dot product of spherical basis tensors tkq:trs
- Cartesian and spherical tensors in NMR Hamiltonian
(top)